Applied Statistics for High-throughput Biology: Session 2

Levi Waldron

Schematic of a typical scRNA-seq analysis workflow

Single-cell workflow

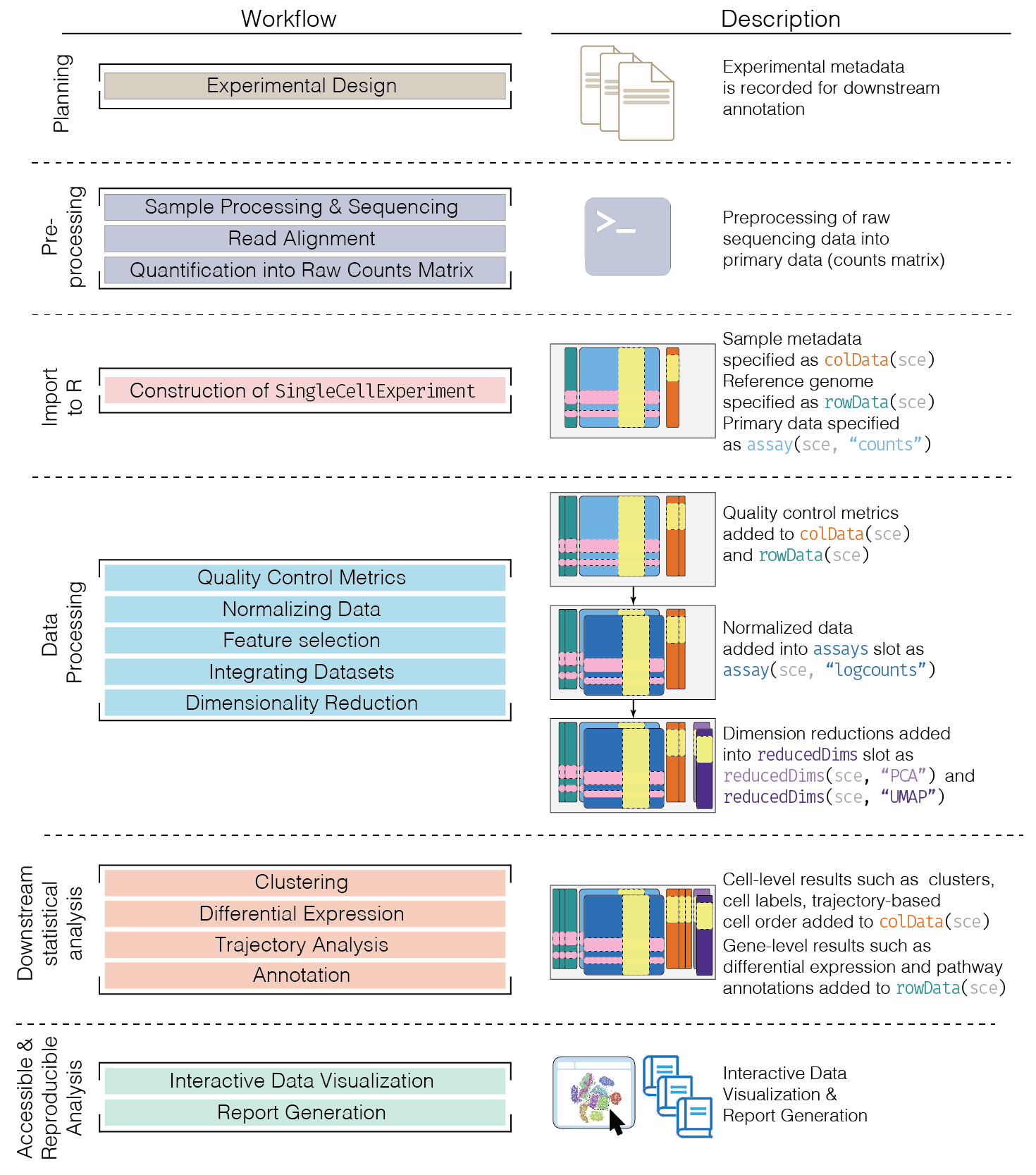
Each stage (separated by dashed lines) consists of a number of specific steps, many of which operate on and modify a SingleCellExperiment instance. (original image)

Day 2 outline

Book chapter 8:

• Distances in high dimensions
• Principal Components Analysis and Singular Value Decomposition
• Multidimensional Scaling
• t-SNE and UMAP

Metrics and distances

A metric satisfies the following five properties:

1. non-negativity $d(a, b) \ge 0$
2. symmetry $d(a, b) = d(b, a)$
3. identification mark $d(a, a) = 0$
4. definiteness $d(a, b) = 0$ if and only if $a=b$
5. triangle inequality $d(a, b) + d(b, c) \ge d(a, c)$

• A distance is only required to satisfy 1-3.
• A similarity function satisfies 1-2, and increases as $a$ and $b$ become more similar
• A dissimilarity function satisfies 1-2, and decreases as $a$ and $b$ become more similar

Euclidian distance (metric)

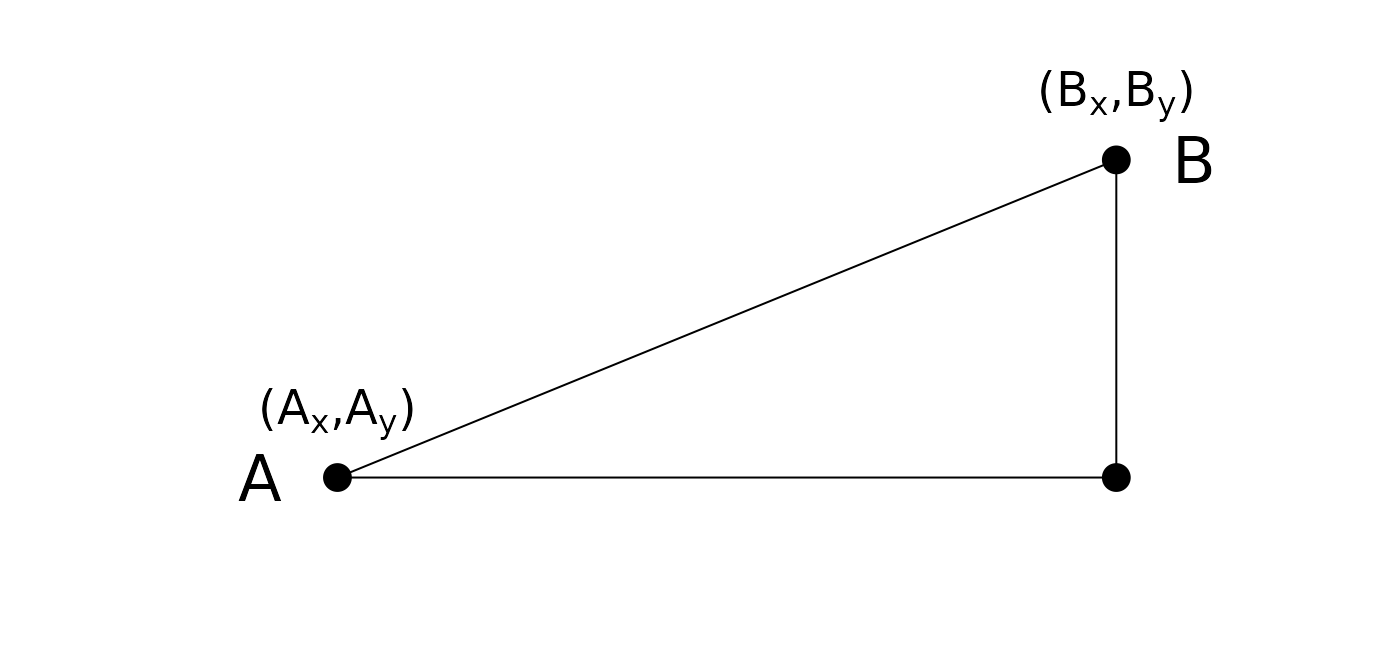
• Remember grade school: Euclidean d = $\sqrt{ (A_x-B_x)^2 + (A_y-B_y)^2}$.
• Side note: also referred to as $L_2$ norm

Euclidian distance in high dimensions

## BiocManager::install("genomicsclass/tissuesGeneExpression") #if needed
## BiocManager::install("genomicsclass/GSE5859") #if needed
library(GSE5859)
library(tissuesGeneExpression)
data(tissuesGeneExpression)
dim(e) ##gene expression data
#> [1] 22215   189
table(tissue) ##tissue[i] corresponds to e[,i]
#> tissue
#>  cerebellum       colon endometrium hippocampus      kidney       liver 
#>          38          34          15          31          39          26 
#>    placenta 
#>           6

Interested in identifying similar samples and similar genes

Notes about Euclidian distance in high dimensions

• Points are no longer on the Cartesian plane
• instead they are in higher dimensions. For example:
  • sample $i$ is defined by a point in 22,215 dimensional space: $(Y_{1,i},\dots,Y_{22215,i})^\top$.
  • feature $g$ is defined by a point in 189 dimensions $(Y_{g,189},\dots,Y_{g,189})^\top$

Euclidean distance as for two dimensions. E.g., the distance between two samples $i$ and $j$ is:

$$\mbox{dist}(i,j) = \sqrt{ \sum_{g=1}^{22215} (Y_{g,i}-Y_{g,j })^2 }$$

and the distance between two features $h$ and $g$ is:

$$\mbox{dist}(h,g) = \sqrt{ \sum_{i=1}^{189} (Y_{h,i}-Y_{g,i})^2 }$$

Euclidian distance in matrix algebra notation

The Euclidian distance between samples $i$ and $j$ can be written as:

$$\mbox{dist}(i,j) = \sqrt{ (\mathbf{Y}_i - \mathbf{Y}_j)^\top(\mathbf{Y}_i - \mathbf{Y}_j) }$$

with $\mathbf{Y}_i$ and $\mathbf{Y}_j$ columns $i$ and $j$.

t(matrix(1:3, ncol = 1))
#>      [,1] [,2] [,3]
#> [1,]    1    2    3
matrix(1:3, ncol = 1)
#>      [,1]
#> [1,]    1
#> [2,]    2
#> [3,]    3
t(matrix(1:3, ncol = 1)) %*% matrix(1:3, ncol = 1)
#>      [,1]
#> [1,]   14

Note about matrix algebra in R

• R is very efficient at matrix algebra
• for very large matricies, see the:
  • Matrix CRAN package (sparse matrices)
  • rhdf5 and DelayedArray Bioconductor package (on-disk arrays)

3 sample example

kidney1 <- e[, 1]
kidney2 <- e[, 2]
colon1 <- e[, 87]
sqrt(sum((kidney1 - kidney2) ^ 2))
#> [1] 85.8546
sqrt(sum((kidney1 - colon1) ^ 2))
#> [1] 122.8919

3 sample example using dist()

dim(e)
#> [1] 22215   189
(d <- dist(t(e[, c(1, 2, 87)])))
#>                 GSM11805.CEL.gz GSM11814.CEL.gz
#> GSM11814.CEL.gz         85.8546                
#> GSM92240.CEL.gz        122.8919        115.4773
class(d)
#> [1] "dist"

The dist() function

Excerpt from ?dist:

dist(
    x,
    method = "euclidean",
    diag = FALSE,
    upper = FALSE,
    p = 2
)

• method: the distance measure to be used.
  • This must be one of “euclidean”, “maximum”, “manhattan”, “canberra”, “binary” or “minkowski”. Any unambiguous substring can be given.
• dist class output from dist() is used for many clustering algorithms and heatmap functions

Caution: dist(e) creates a 22215 x 22215 matrix that will probably crash your R session.

Note on standardization

• In practice, features (e.g. genes) are typically “standardized”, i.e. converted to z-score:

$$x_{gi} \leftarrow \frac{(x_{gi} - \bar{x}_g)}{s_g}$$

• This is done because the differences in overall levels between features are often not due to biological effects but technical ones, e.g.:
  • GC bias, PCR amplification efficiency, …

Dimension reduction and PCA

• Motivation for dimension reduction

Simulate the heights of twin pairs:

set.seed(1)
n <- 100
y <- t(MASS::mvrnorm(n, c(0, 0), matrix(c(1, 0.95, 0.95, 1), 2, 2)))
dim(y)
#> [1]   2 100
cor(t(y))
#>           [,1]      [,2]
#> [1,] 1.0000000 0.9433295
#> [2,] 0.9433295 1.0000000

Visualizing twin pairs data

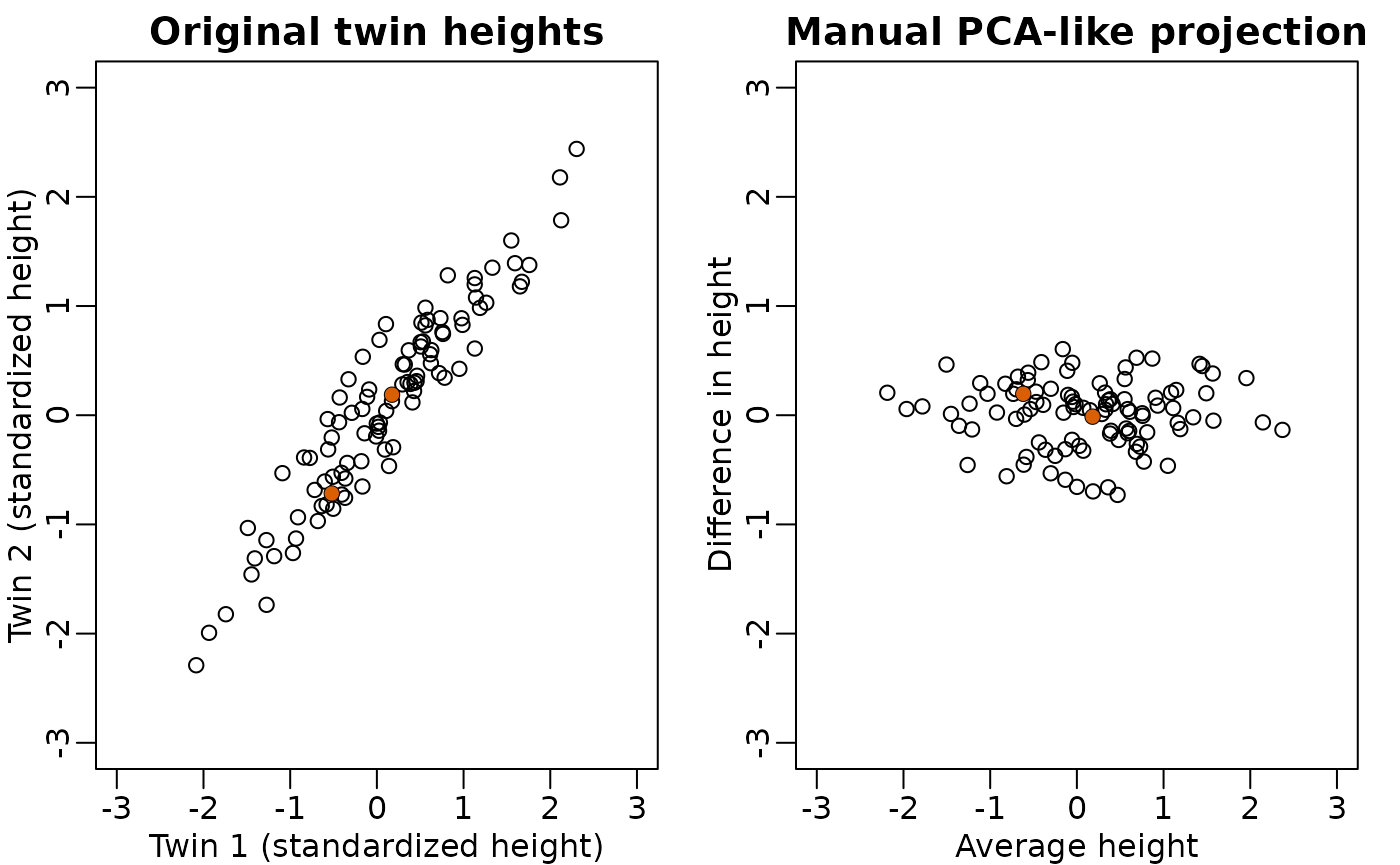
Not much distance is lost in the second dimension

• Not much loss of height differences when just using average heights of twin pairs.
  • because twin heights are highly correlated

Singular Value Decomposition (SVD)

SVD generalizes the example rotation we looked at:

$$\mathbf{Y} = \mathbf{UDV}^\top$$

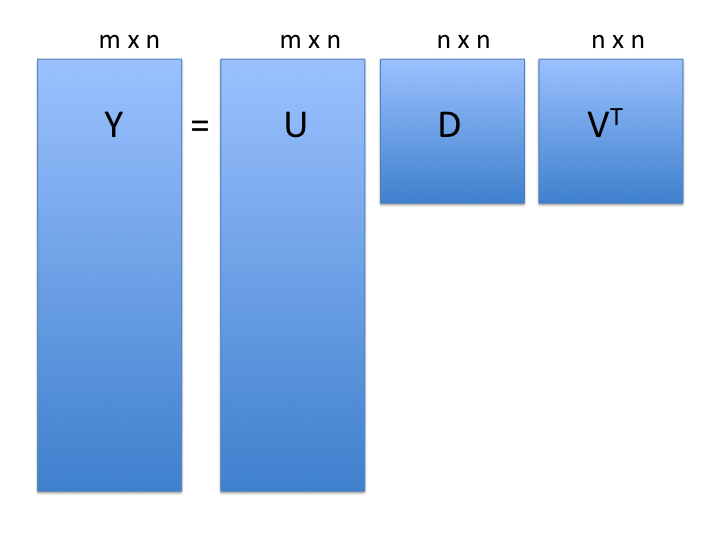
• note: the above formulation is for $m$ rows $> n$ columns

• $\mathbf{Y}$: the $m$ rows x $n$ cols matrix of measurements

• $\mathbf{U}$: $m \times n$ matrix relating original scores to PCA scores (loadings)

• $\mathbf{D}$: $n \times n$ diagonal matrix (eigenvalues)

• $\mathbf{V}$: $n \times n$orthogonal matrix (eigenvectors or PCA scores)

  • orthogonal = unit length and “perpendicular” in 3-D

SVD of gene expression dataset

Center but do not scale, just to make plots before more legible:

e.standardize <- t(scale(t(e), scale = FALSE))

SVD:

s <- svd(e.standardize)
names(s)
#> [1] "d" "u" "v"

Components of SVD results

dim(s$u)     # loadings
#> [1] 22215   189
length(s$d)  # eigenvalues
#> [1] 189
dim(s$v)     # d %*% vT = scores
#> [1] 189 189

PCA is a SVD

• gene expression dataset

rafalib::mypar()
p <- prcomp(t(e.standardize))
plot(s$u[, 1] ~ p$rotation[, 1])

Lesson: u and v can each be multiplied by -1 arbitrarily

PCA interpretation: loadings

• $\mathbf{U}$ (loadings): relate the principal component axes to the original variables
  • think of principal component axes as a weighted combination of original axes

Visualizing PCA loadings

plot(p$rotation[, 1],
     xlab = "Index of genes",
     ylab = "Loadings of PC1",
     main = "PC1 loadings of each gene") #or, predict(p)
abline(h = c(-0.03, 0.03), col = "red")

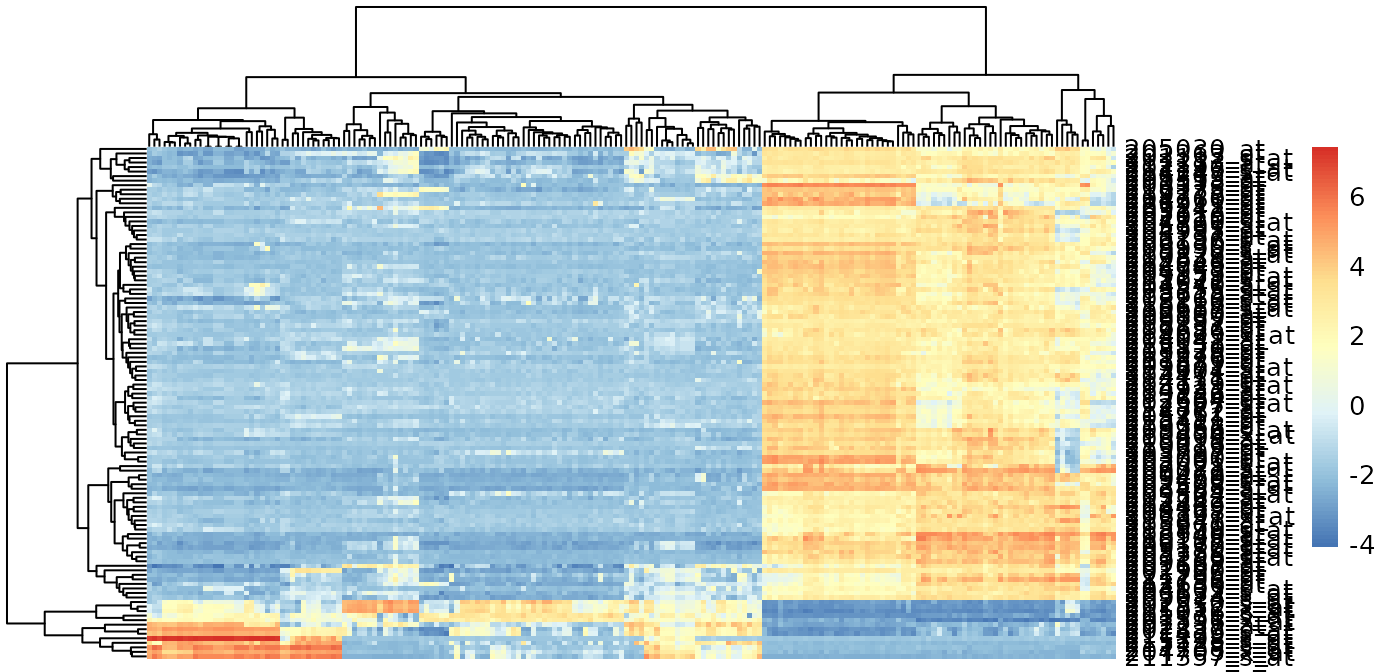
Genes with high PC1 loadings

e.pc1genes <-
    e.standardize[p$rotation[, 1] < -0.03 |
                           p$rotation[, 1] > 0.03,]
pheatmap::pheatmap(
    e.pc1genes,
    scale = "none",
    show_rownames = TRUE,
    show_colnames = FALSE
)

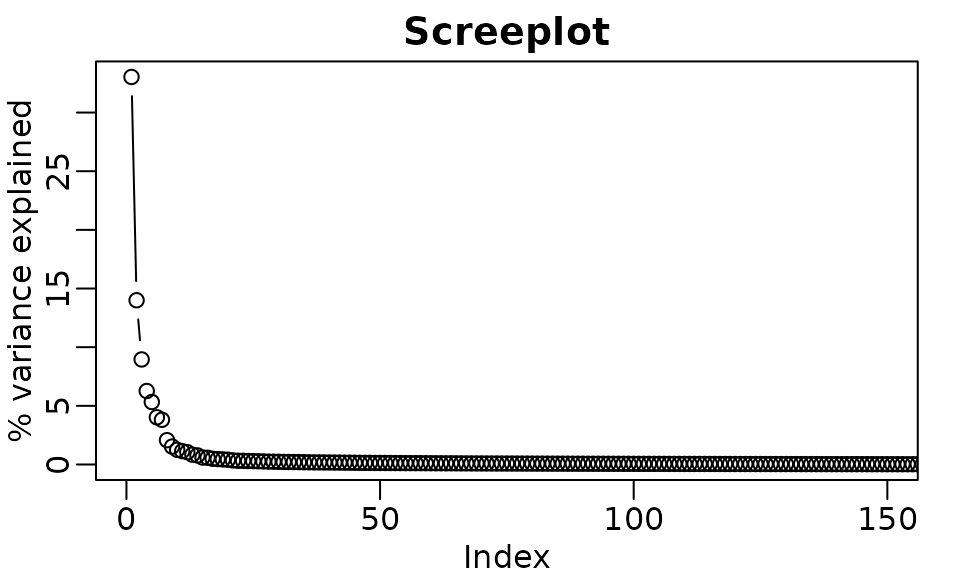
PCA interpretation: eigenvalues

• $\mathbf{D}$ (eigenvalues): standard deviation scaling factor that each decomposed variable is multiplied by.

rafalib::mypar()
plot(
    p$sdev ^ 2 / sum(p$sdev ^ 2) * 100,
    xlim = c(0, 150),
    type = "b",
    ylab = "% variance explained",
    main = "Screeplot"
)

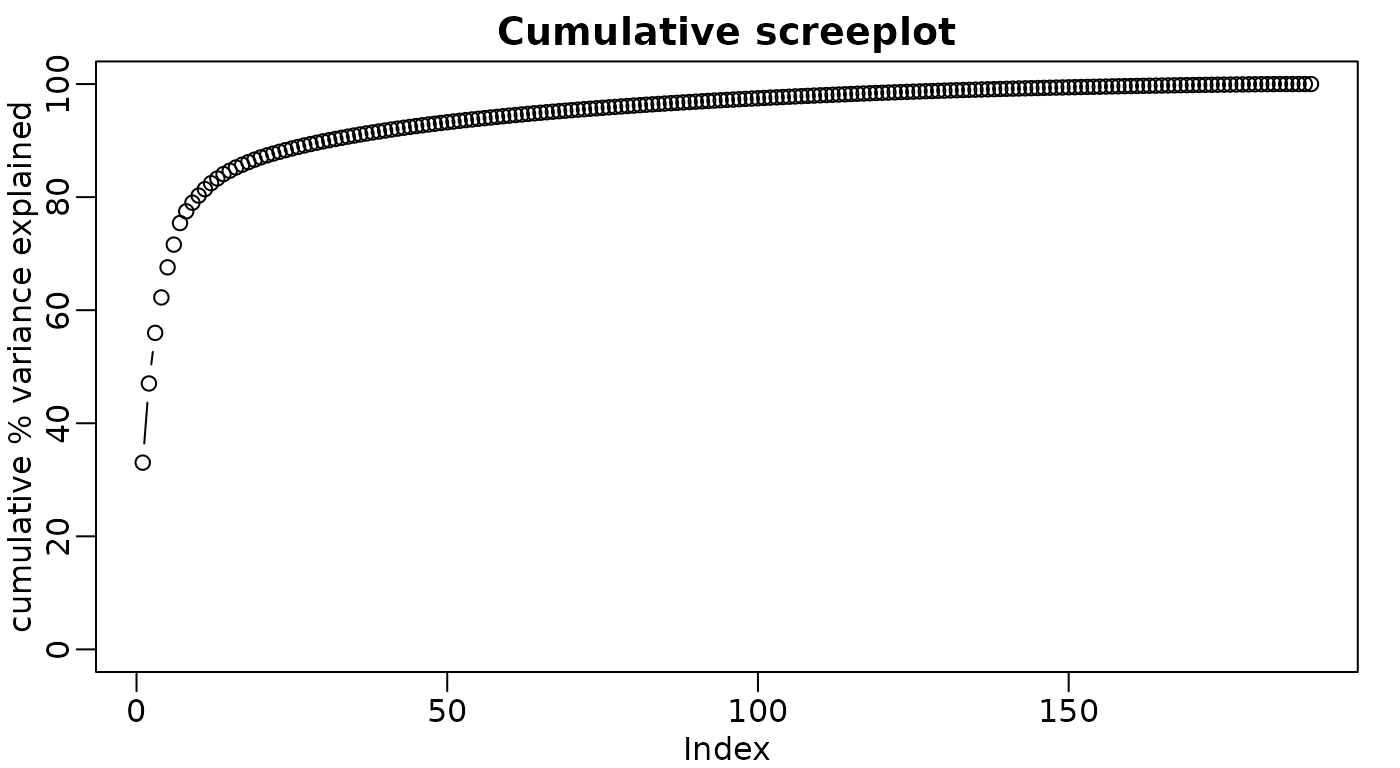
PCA interpretation: eigenvalues

Alternatively as cumulative % variance explained (using cumsum() function)

rafalib::mypar()
plot(
    cumsum(p$sdev ^ 2) / sum(p$sdev ^ 2) * 100,
    ylab = "cumulative % variance explained",
    ylim = c(0, 100),
    type = "b",
    main = "Cumulative screeplot"
)

PCA interpretation: scores

• $\mathbf{V}$ (scores): The “datapoints” in the reduced prinipal component space
• In some implementations (like prcomp()), scores are already scaled by eigenvalues: $\mathbf{D V^T}$

PCA interpretation: scores

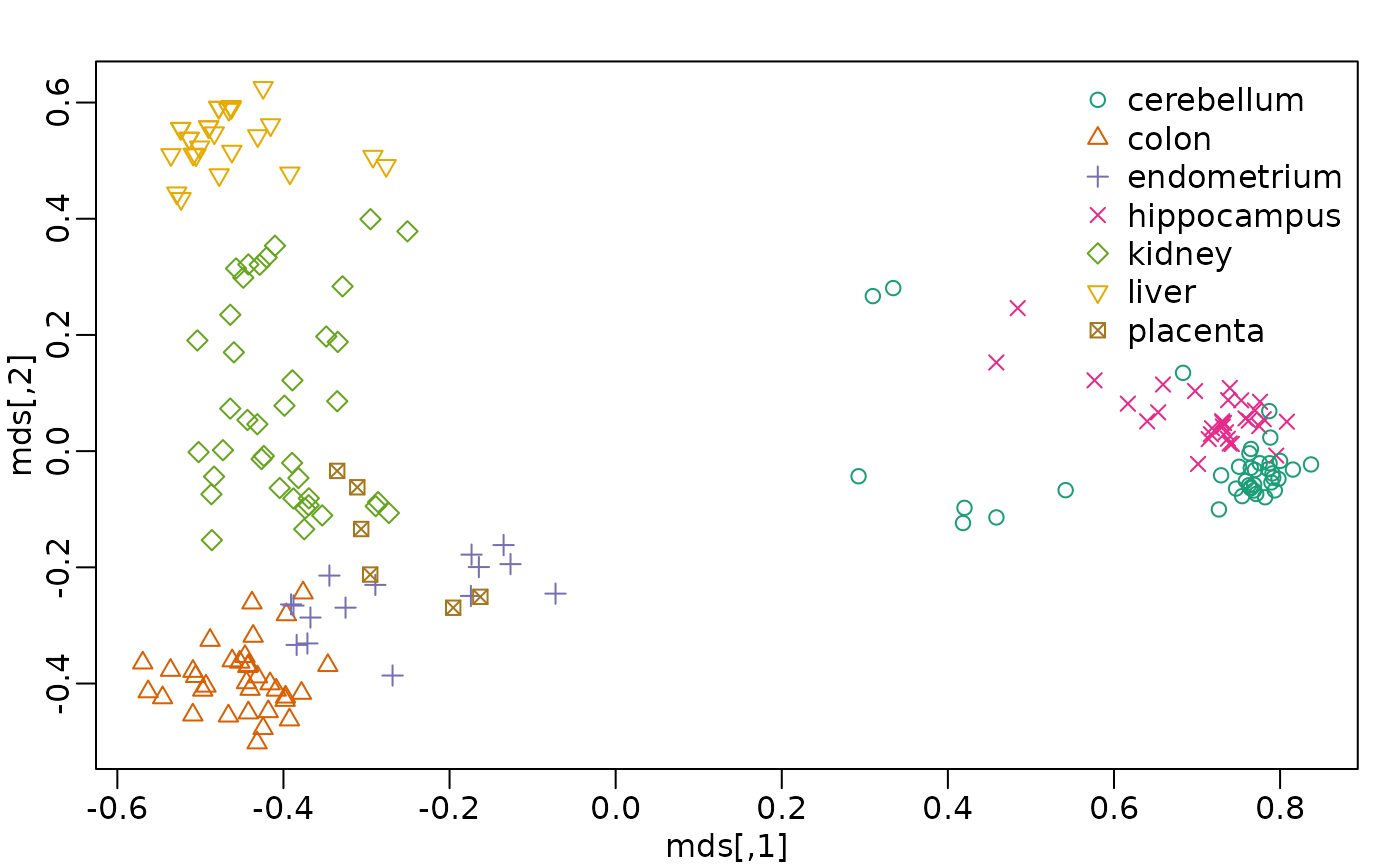
Multi-dimensional Scaling (MDS)

• also referred to as Principal Coordinates Analysis (PCoA)
• a reduced SVD, performed on a distance matrix
• identify two (or more) eigenvalues/vectors that preserve distances

d <- as.dist(1 - cor(e.standardize))
mds <- cmdscale(d)

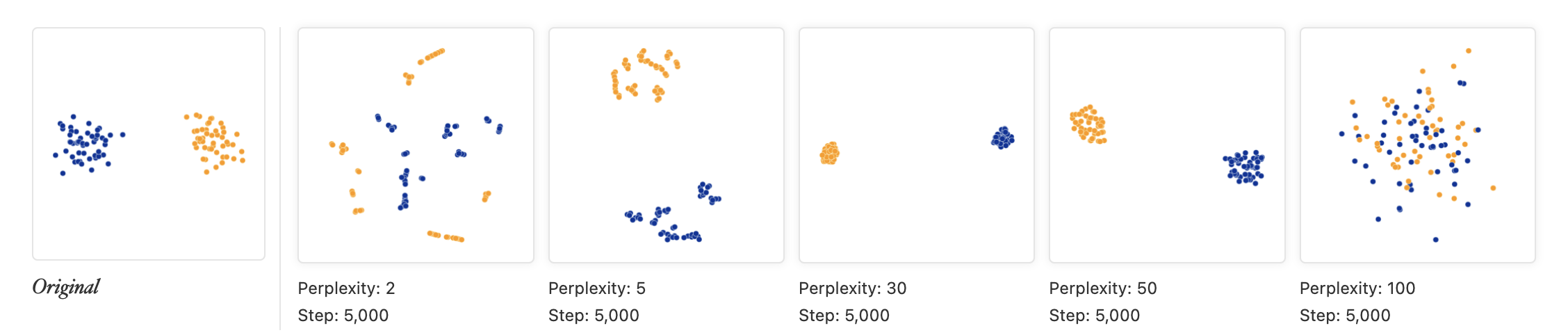
t-SNE

• non-linear dimension reduction method very popular for visualizing single-cell data
  • almost magical ability to show clearly separated clusters
  • performs different transformations on different regions
• computationally intensive so usually done only on top ~30 PCs
• t-SNE is sensitive to choices of tuning parameters
  • “perplexity” parameter defines (loosely) how to balance attention between local and global aspects of data
  • optimal choice of perplexity changes for different numbers of cells from the same sample.
  • perplexity = $\sqrt{N}$ is one rule of thumb. $max(N/5, 50)$ is another (default of Rtsne)
  • Here is a good post by Nikolay Oskolkov on this topic.

t-SNE caveats

• uses a random number generator
• apparent spread of clusters is completely meaningless
• distance between clusters might also not mean anything
• parameters can be tuned to make data appear how you want
• can show apparent clusters in random noise. Should not be used for statistical inference
• Try it to gain some intuition: https://distill.pub/2016/misread-tsne/)

tSNE

PCA of Zeisel single-cell RNA-seq dataset

sce.zeisel <- fixedPCA(sce.zeisel, subset.row=NULL)
plotReducedDim(sce.zeisel, dimred="PCA", colour_by="level1class")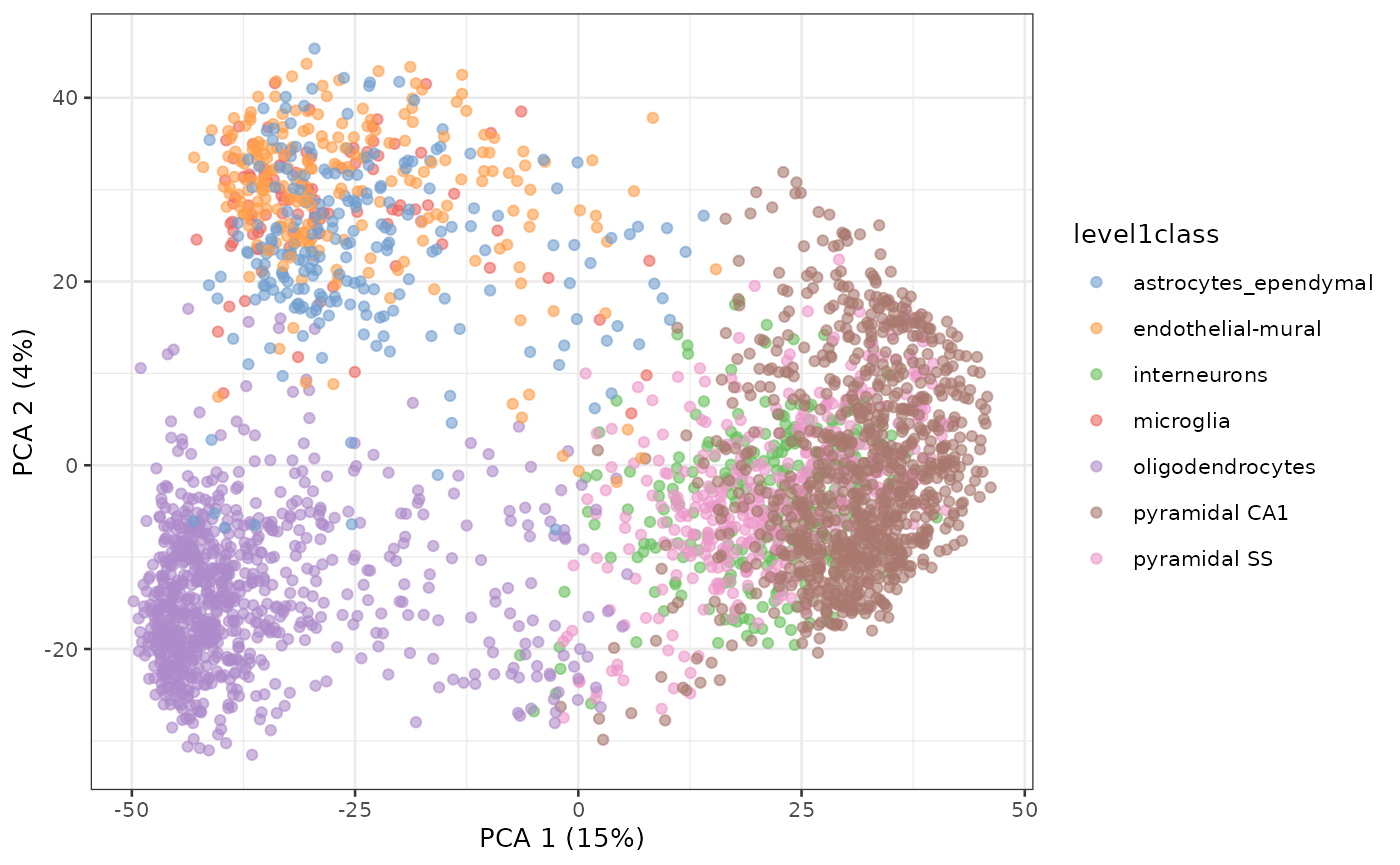

Principal Components Analysis of Zeisel dataset

t-SNE of the same dataset

sce.zeisel <- runTSNE(sce.zeisel, dimred="PCA")
plotReducedDim(sce.zeisel, dimred="TSNE", colour_by="level1class")

t-SNE clustering of Zeisel dataset

UMAP vs t-SNE

• UMAP may better preserve local and global distances
• tends to have more compact visual clusters with more empty space between them
• more computationally efficient
• also involves random number generation
• Note: I prefer not setting the random number seed during exploratory analysis in order to see the random variability

UMAP of the same dataset

sce.zeisel <- runUMAP(sce.zeisel, dimred="PCA")
plotReducedDim(sce.zeisel, dimred="UMAP", colour_by="level1class")

UMAP representation of the Zeisel dataset

tSNE of tissue microarray data

Using default parameters and no log transformation

sct <- SingleCellExperiment(e)
sct$tissue <- tissue
# fake the log normalization because it is undesirable for microarray data
names(assays(sct)) <- "logcounts" 
sct <- fixedPCA(sct, subset.row=NULL)
sct <- runTSNE(sct, dimred="PCA")
plotReducedDim(sct, dimred="TSNE", colour_by="tissue")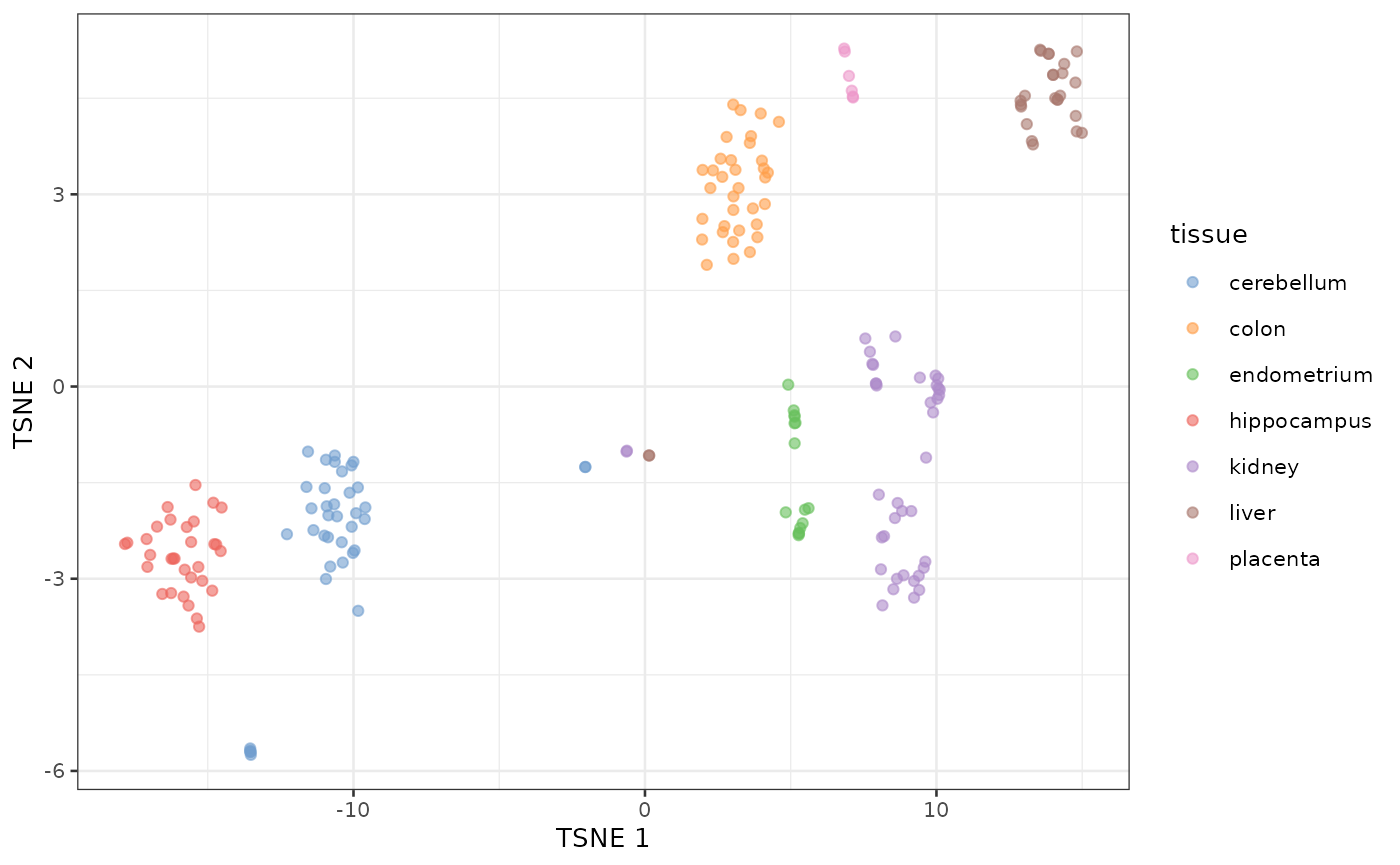

UMAP of tissue microarray data

Also using default parameters and no log transformation

sct <- runUMAP(sct, dimred="PCA")
plotReducedDim(sct, dimred="UMAP", colour_by="tissue")

Summary: distances and dimension reduction

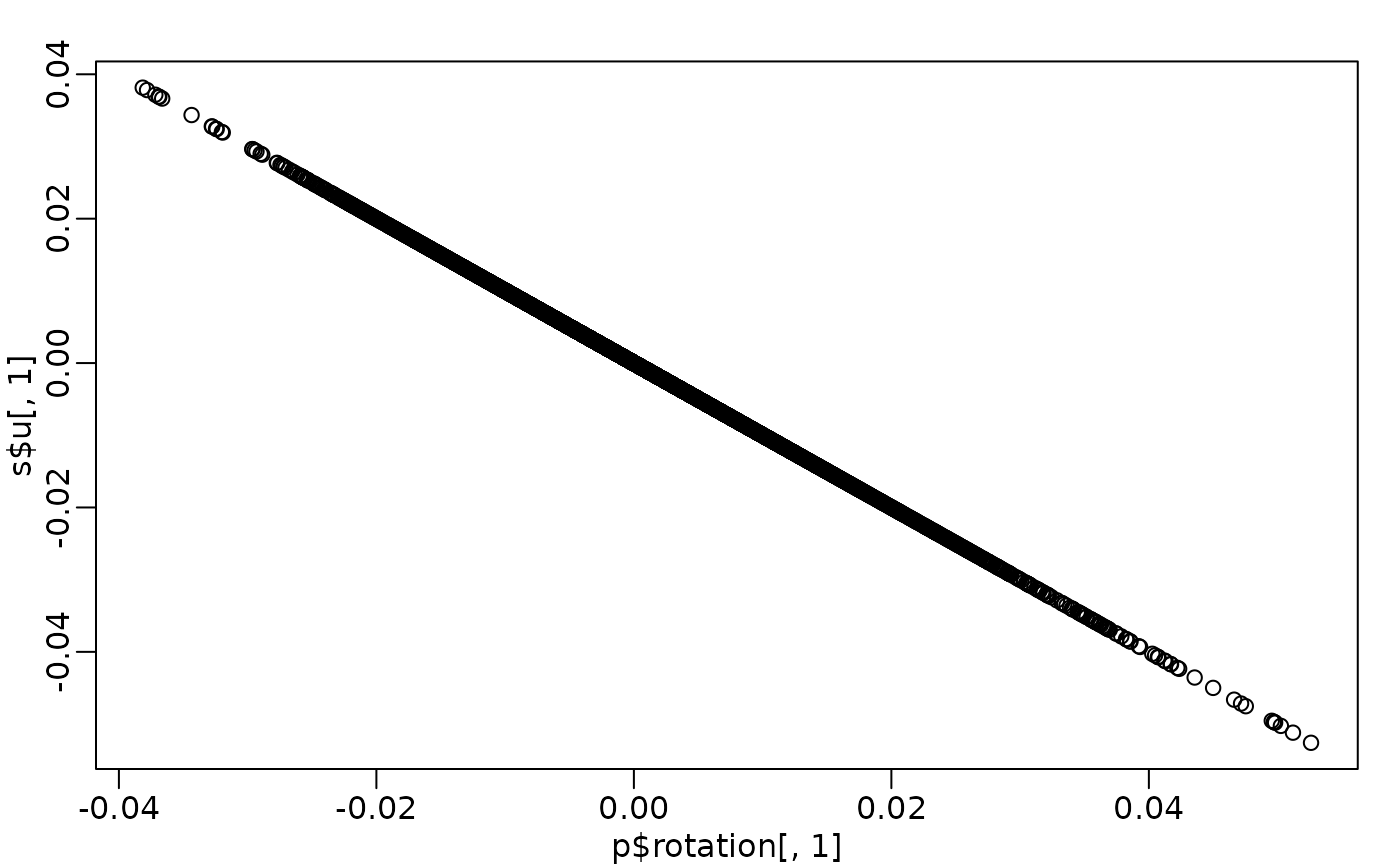
• Note: signs of rotations (loadings) and eigenvectors (scores) can be arbitrarily flipped
• PCA and MDS are useful for dimension reduction when you have correlated variables
• Variables are always centered.
  
• Variables are also scaled unless you know they have the same scale in the population
• PCA projection can be applied to new datasets if you know the matrix calculations
• PCA is subject to over-fitting, screeplot can be tested by cross-validation
• PCA is often used prior to t-SNE and UMAP for de-noising and computational tractability

Lab exercise

• OSCA Basics: Chapter 4 Dimensionality Reduction
• Optional if you are interested, OSCA Advanced: Chapter 4 Dimensionality reduction, redux

Links

• A built html version of this lecture is available.
• The source R Markdown is also available from Github.