Applied Statistics for High-throughput Biology: Session 1 • AppStatBio

Front matter

Welcome

My research interests:

High-dimensional statistics (more variables than observations)
Predictive modeling and methodology for validation
Metagenomic profiling of the human microbiome
Multi-omic data analysis for cancer
https://www.waldronlab.io

The textbooks

Biomedical Data Science by Irizarry and Love (ePub version on Leanpub)
Source repository
Modern Statistics for Modern Biology by Holmes and Huber (secondary)
Orchestrating Single-Cell Analysis with Bioconductor (OSCA) by Amezquita, Lun, Hicks, Gottardo, O’Callaghan

Biomedical Data Science book cover

Day 1 outline

Random variables and distributions
Hypothesis testing for one or two samples (t-test, Wilcoxon test, etc)
Confidence intervals
Essential data classes in R/Bioconductor
Book chapters 0 and 1

Learning objectives

Define random variables and distinguish them from non-random ones
Distinguish population from sampling distributions
Identify scenarios for use of z-test and t-tests
Interpret confidence intervals and Standard Error
Identify and interrogate key R/Bioconductor data classes

Random Variables and Distributions

Random Variables

A random variable: any characteristic that can be measured or categorized, and where any particular outcome is determined at least partially by chance.
Examples:
- number of new diabetes cases in population in a given year
- The weight of a randomly selected individual in a population
Types:
- Categorical random variable (e.g. disease / healthy)
- Discrete random variable (e.g. sequence read counts)
- Continuous random variable (e.g. normalized qPCR intensity)

Random Variables - examples

Normally distributed random variable with mean $\mu = 0$ / standard deviation $\sigma = 1$ , and a sample of $n=100$

Random Variables - examples

Poisson distributed random variable ( $\lambda = 2$ ), and a sample of $n=100$ .

Random Variables - examples

Negative Binomially distributed random variable ( $size=30, \mu=2$ ), and a sample of $n=100$ .

Random Variables - examples

Binomial Distribution random variable (size=20,prob=0.25size=20, prob=0.25), and a sample of n=100n=100.
- use for binary outcomes

Hypothesis Testing

Why hypothesis testing?

Allows yes/no statements, e.g. whether:
- a population mean has a hypothesized value, or
- an intervention causes a measurable effect relative to a control group
Example questions with yes/no answers:
- Is a gene differentially expressed between two populations?
- Do hypertensive, smoking men have the same mean cholesterol level as the general population?
Hypothesis testing is not the only framework for inferential statistics, e.g.:
- confidence intervals
- posterior probabilities (Bayesian statistics)
- read p-values are just the tip of the iceberg

Logic of hypothesis testing

Hypotheses are made about populations based on inference from samples
We make inference from samples because we usually cannot observe the entire population

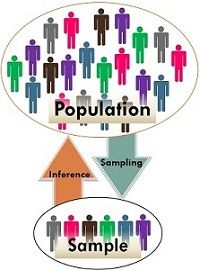
Sample vs Population

Source: https://keydifferences.com/wp-content/uploads/2016/06/population-vs-sample2.jpg

One and two-sample hypothesis tests of mean

One-sample hypothesis test of mean - sample comes from one of two population distributions:

usual distribution that has been true in the past
- $H_0: \mu = \mu_0$ (null hypothesis)
a potentially new distribution induced by an intervention or changing condition
- $H_A: \mu \neq \mu_0$ (alternative hypothesis)

Two-sample hypothesis test of means - two samples are drawn, either:

from a single population
- $H_0: \mu_1 = \mu_2$ (null hypothesis)
from two different populations
- $H_A: \mu_1 \neq \mu_2$ (alternative hypothesis)

Population vs sampling distributions

Population distributions
- Each realization / point is an individual
Sampling distributions
- Each realization / point is a sample
- distribution depends on sample size
- large sample distributions are given by the Central Limit Theorem
Hypothesis testing is about sampling distributions
- Did my sample likely come from that distribution?

Note about the Central Limit Theorem

When sample size is large, the average $\bar{Y}$ of a random sample:

Follows a normal distribution
The normal distribution has mean entered at the population average $\mu_Y$
with standard deviation equal to the population standard deviation $\sigma_Y$ , divided by the square root of the sample size $N$ . We refer to the standard deviation of the distribution of a random variable as the random variable’s standard error.

Thanks to CLT, linear modeling, t-tests, ANOVA are all guaranteed to work reasonably well for large samples (more than ~30 observations).

Go to online demo: http://onlinestatbook.com/stat_sim/sampling_dist/

Example applications of hypothesis tests for continuous variables

Do study participants on a diet lose weight compared to a control group?
Does a gene knockout result in less viable cell colonies, as measured by the number of living cells in replicate experiments?
Is Prevotella copri more abundant in the guts of vegans than of meat-eaters?
Do infants born in this region have a higher birthweight than the national average?

These are research hypotheses. What are the corresponding null hypotheses?

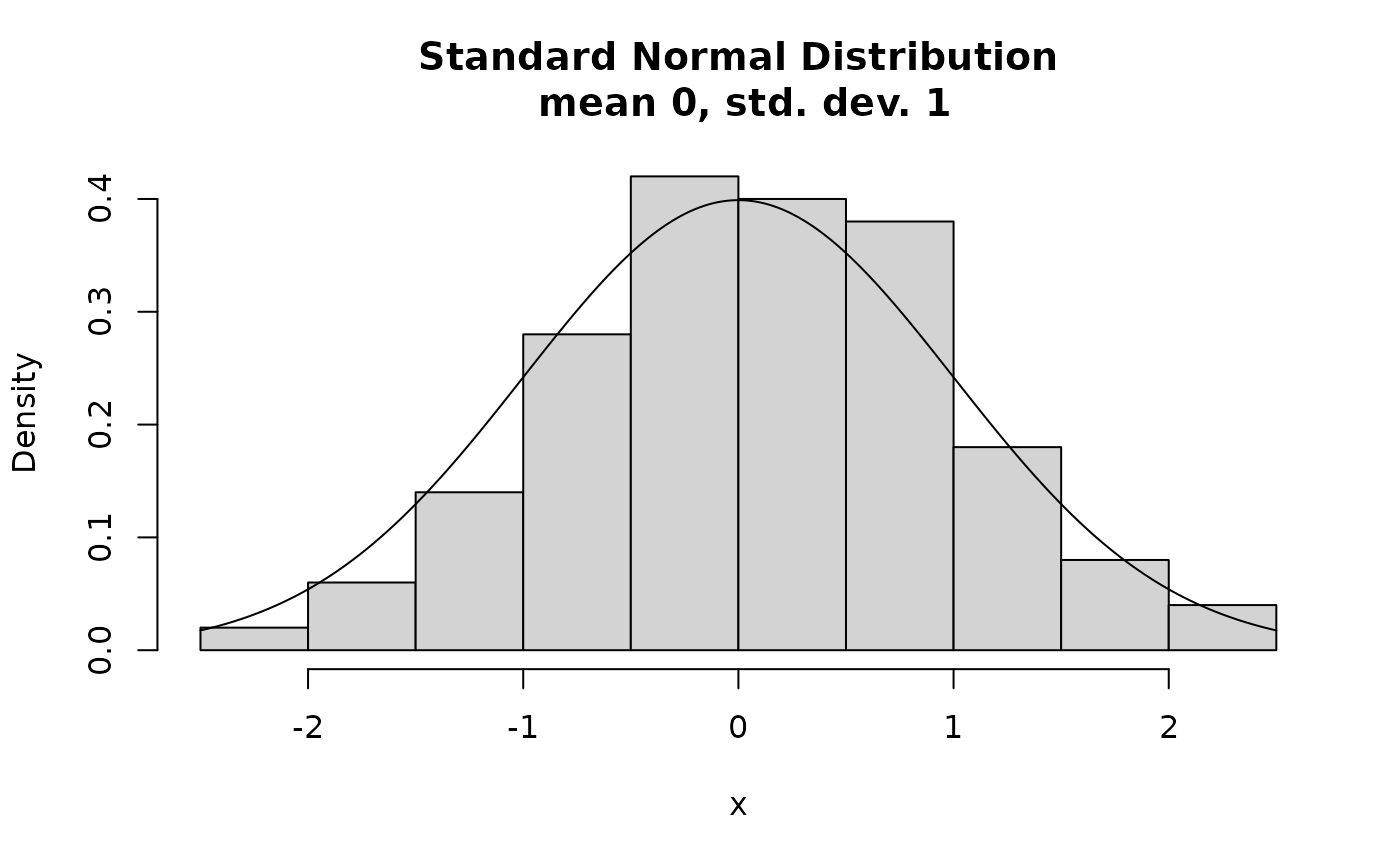
The z-tests

“ $z$ ” refers to the Standard Normal Distribution: $N(\mu=0, \sigma=1)$
In a one-sample test, only a single sample is drawn:
- $H_0: \mu = \mu_0$
In a two-sample test, two samples are drawn independently:
- $H_0: \mu_1 = \mu_2$
A paired test is one sample of paired measurements, e.g.:
- pain level in individuals before and after treatment
  - $H_0: \mu_{before} = \mu_{after}$
- microbial abundance in upper and lower intestines in same individuals
  - $H_0: \mu_{upper} = \mu_{lower}$

When to use z-tests

x‾−μσ\frac{{}\bar{x} - \mu}{\sigma} and x1‾−x2‾σ\frac{\bar{x_1} - \bar{x_2}}{\sigma} are z-distributed if:
- the standard deviation $\sigma$ for the population is known in advance
- the population values are normally distributed
- the population values are slightly skewed but n > 15
- the population values are quite skewed but n > 30

Example of one-sample z-test

library(TeachingDemos)
set.seed(1)
(weights = rnorm(10, mean = 75, sd = 10))
#>  [1] 68.73546 76.83643 66.64371 90.95281 78.29508 66.79532 79.87429 82.38325
#>  [9] 80.75781 71.94612
TeachingDemos::z.test(
    x = weights,
    mu = 70,  #specified for population under H0 because this is a one-sample test
    stdev = 10, #specified for population because this is a z-test
    alternative = "two.sided"
)
#> 
#>  One Sample z-test
#> 
#> data:  weights
#> z = 1.9992, n = 10.0000, Std. Dev. = 10.0000, Std. Dev. of the sample
#> mean = 3.1623, p-value = 0.04559
#> alternative hypothesis: true mean is not equal to 70
#> 95 percent confidence interval:
#>  70.12408 82.51998
#> sample estimates:
#> mean of weights 
#>        76.32203

The t-tests

The t-tests are for small samples and do not rely on the Central Limit Theorem
In a one-sample test, only a single sample is drawn:
- $H_0: \mu = \mu_0$
In a two-sample test, two samples are drawn independently:
- $H_0: \mu_1 = \mu_2$
A paired test is one sample of paired measurements, e.g.:
- individuals before and after treatment

When to use t-tests

x‾−μs\frac{{}\bar{x} - \mu}{s} and x1‾−x2‾s\frac{\bar{x_1} - \bar{x_2}}{s} are t-distributed if:
- the standard deviation $s$ is estimated from the sample
- the population values are normally distributed
- the population values are slightly skewed but n > 15
- the population values are quite skewed but n > 30
Wilcoxon tests are an alternative for non-normal populations
- e.g. rank data
- data where ranks are more informative than means
- not when many ranks are arbitrary

Example of one-sample t-test

Note that here we do not specify the standard deviation, because it is estimated from the sample.

stats::t.test(
    x = weights,
    mu = 70,  #specified for population under H0 because this is a one-sample test
    alternative = "two.sided"
)
#> 
#>  One Sample t-test
#> 
#> data:  weights
#> t = 2.5612, df = 9, p-value = 0.03063
#> alternative hypothesis: true mean is not equal to 70
#> 95 percent confidence interval:
#>  70.73805 81.90600
#> sample estimates:
#> mean of x 
#>  76.32203

In this particular example the p-value is smaller than from the z-test, but in general it would be less powerful than a z-test if its assumptions are met.

Confidence intervals

Why confidence intervals?

The above procedures produced both p-values and confidence intervals
p-values are useful only for deciding whether to reject $H_0$
p-values do not report effect size (observed difference).
p-values only indicate statistical significance which does not guarantee scientific/clinical significance.

Confidence intervals provide a probable range for the true population mean.

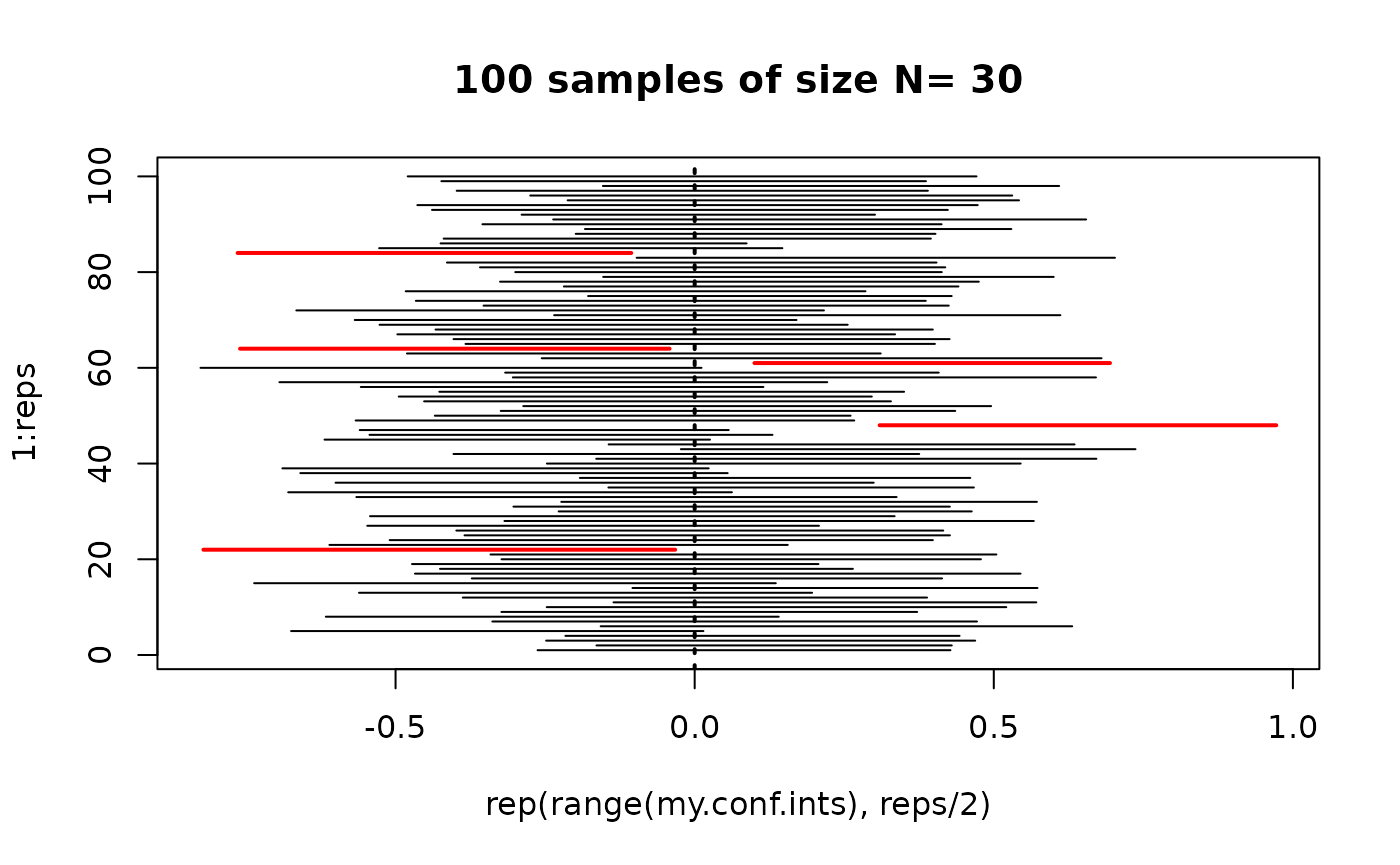
Intervals for any confidence level

If the sampling distribution is normal with standard error SESE, then a confidence interval for the population mean is:
- $\bar{X} \pm 1.96 \times SE$ (95% CI, normal sampling distribution)
- $\bar{X} \pm z_{\alpha / 2}^{crit} \times SE$ (normal sampling distribution)
- $\bar{X} \pm t_{\alpha / 2, df}^{crit} \times SE$ (t sampling distribution)
The part after the $\pm$ is called the margin of error

Confidence intervals vs. hypothesis testing

Confidence intervals can be used for hypothesis testing
- reject $H_0$ if the “null value” is not contained in the CI
Do not use overlap between two CIs for hypothesis test
- for a two sample hypothesis test $H_0: \mu_1 = \mu_2$ , must construct a single confidence interval for $\mu_1 - \mu_2$

Q & A: confidence intervals

Which of the following are true?

The 95% CI contains 95% of the values in the population
The 95% CI will contain the population mean, 19 times out of 20
The 95% CI is 95% probable to contain the population mean
The 99% CI will be wider than the 95% CI

Summary - hypothesis testing

Power and type I and II error

True state of nature	Result of test
	Reject $H_0$	Fail to reject $H_0$
$H_0$ TRUE	Type I error, probability = $\alpha$	No error, probability = $1-\alpha$
$H_0$ FALSE	No error, probability is called power = $1-\beta$	Type II error, probability = $\beta$ (false negative)

Use and mis-use of the p-value

The p-value is the probability of observing a sample statistic as or more extreme as you did, assuming that $H_0$ is true
The p-value is a random variable:
- don’t treat it as precise.
- don’t do silly things like try to interpret differences or ratios between p-values
- don’t lose track of test assumptions such as independence of observations
- do use a moderate p-value cutoff, then use some effect size measure for ranking
Small p-values are particularly:
- variable under repeated sampling, and
- sensitive to test assumptions

Use and mis-use of the p-value (cont’d)

If we fail to reject H0H_0, is the probability that H0H_0 is true equal to (1−α1-\alpha)? (Hint: NO NO NO!)
- Failing to reject $H_0$ does not mean $H_0$ is true
- “No evidence of difference $\neq$ evidence of no difference”
Statistical significance vs. practical significance
- As sample size increases, point estimates such as the mean are more precise
- With large sample size, small differences in means may be statistically significant but not practically significant
Although $\alpha = 0.05$ is a common cut-off for the p-value, there is no set border between “significant” and “insignificant,” only increasingly strong evidence against $H_0$ (in favor of $H_A$ ) as the p-value gets smaller.

R - basic usage

Tips for learning R

Pseudo code	Example code
library(packagename)	library(dplyr)
?functionname	?select
?package::functionname	?dplyr::select
? ‘Reserved keyword or symbol’	? ‘%>%’
??searchforpossiblyexistingfunctionandortopic	??simulate
help(package = “loadedpackage”)	help(“dplyr”)
browseVignettes(“packagename”)	browseVignettes(“dplyr”)

Slide credit: Marcel Ramos

Installing Packages the Bioconductor Way

See the Bioconductor site for more info

Pseudo code:

install.packages("BiocManager") #from CRAN
packages <- c("packagename", "githubuser/repository", "biopackage")
BiocManager::install(packages)
BiocManager::valid()  #check validity of installed packages

Works for CRAN, GitHub, and Bioconductor packages!

Introduction to the R/Bioconductor data classes

Base R Data Types: atomic vectors

numeric (set seed to sync random number generator):

set.seed(1)
rnorm(5)
#> [1] -0.6264538  0.1836433 -0.8356286  1.5952808  0.3295078

integer:

sample(1L:5L)
#> [1] 3 5 1 4 2

logical:

1:3 %in% 3
#> [1] FALSE FALSE  TRUE

character:

c("yes", "no")
#> [1] "yes" "no"

factor:

factor(c("yes", "no"))
#> [1] yes no 
#> Levels: no yes

For real-life recoding of factors, try dplyr::recode, dplyr::recode_factor

Base R Data Types: missingness

Missing Values and others - IMPORTANT

c(NA, NaN, -Inf, Inf)
#> [1]   NA  NaN -Inf  Inf

class() to find the class of a variable.

Base R Data Types: matrix, list, data.frame

matrix:

matrix(1:9, nrow = 3)
#>      [,1] [,2] [,3]
#> [1,]    1    4    7
#> [2,]    2    5    8
#> [3,]    3    6    9

The list is a non-atomic vector:

measurements <- c(1.3, 1.6, 3.2, 9.8, 10.2)
parents <- c("Parent1.name", "Parent2.name")
my.list <- list(measurements, parents)
my.list
#> [[1]]
#> [1]  1.3  1.6  3.2  9.8 10.2
#> 
#> [[2]]
#> [1] "Parent1.name" "Parent2.name"

The data.frame has list-like and matrix-like properties:

x <- 11:16
y <- seq(0, 1, .2)
z <- c("one", "two", "three", "four", "five", "six")
a <- factor(z)
my.df <- data.frame(x, y, z, a, stringsAsFactors = FALSE)

Bioconductor S4 vectors: DataFrame

Bioconductor (www.bioconductor.org) defines its own set of vectors using the S4 formal class system DqtqFrame: like a data.frame but more flexible. columns can be any atomic vector type:
- GenomicRanges objects
- Rle (run-length encoding)

suppressPackageStartupMessages(library(S4Vectors))
df <- DataFrame(var1 = Rle(c("a", "a", "b")),
                var2 = 1:3)
metadata(df) <- list(parent = "DataFrame is my virtual parent")
df
#> DataFrame with 3 rows and 2 columns
#>    var1      var2
#>   <Rle> <integer>
#> 1     a         1
#> 2     a         2
#> 3     b         3

DataFrame is actually a virtual classes

Rationale: Methods defined on DFrame are shared by all classes inheriting it
See: https://bioconductor.org/help/course-materials/2019/BiocDevelForum/02-DataFrame.pdf
See also: https://github.com/Bioconductor/S4Vectors/issues/90#issue-1026425148

List and derived classes

List(my.list)
#> List of length 2
str(List(my.list))
#> Formal class 'SimpleList' [package "S4Vectors"] with 4 slots
#>   ..@ listData       :List of 2
#>   .. ..$ : num [1:5] 1.3 1.6 3.2 9.8 10.2
#>   .. ..$ : chr [1:2] "Parent1.name" "Parent2.name"
#>   ..@ elementType    : chr "ANY"
#>   ..@ elementMetadata: NULL
#>   ..@ metadata       : list()

suppressPackageStartupMessages(library(IRanges))
IntegerList(var1 = 1:26, var2 = 1:100)
#> IntegerList of length 2
#> [["var1"]] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
#> [["var2"]] 1 2 3 4 5 6 7 8 9 10 11 12 ... 89 90 91 92 93 94 95 96 97 98 99 100
CharacterList(var1 = letters[1:100], var2 = LETTERS[1:26])
#> CharacterList of length 2
#> [["var1"]] a b c d e f g h i j ... <NA> <NA> <NA> <NA> <NA> <NA> <NA> <NA> <NA>
#> [["var2"]] A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
LogicalList(var1 = 1:100 %in% 5, var2 = 1:100 %% 2)
#> LogicalList of length 2
#> [["var1"]] FALSE FALSE FALSE FALSE TRUE FALSE ... FALSE FALSE FALSE FALSE FALSE
#> [["var2"]] TRUE FALSE TRUE FALSE TRUE FALSE ... FALSE TRUE FALSE TRUE FALSE

Biostrings

suppressPackageStartupMessages(library(Biostrings))
bstring <- BString("I am a BString object")
bstring
#> 21-letter BString object
#> seq: I am a BString object

dnastring <- DNAString("TTGAAA-CTC-N")
dnastring
#> 12-letter DNAString object
#> seq: TTGAAA-CTC-N
str(dnastring)
#> Formal class 'DNAString' [package "Biostrings"] with 5 slots
#>   ..@ shared         :Formal class 'SharedRaw' [package "XVector"] with 2 slots
#>   .. .. ..@ xp                    :<externalptr> 
#>   .. .. ..@ .link_to_cached_object:<environment: 0x5630d2d39d48> 
#>   ..@ offset         : int 0
#>   ..@ length         : int 12
#>   ..@ elementMetadata: NULL
#>   ..@ metadata       : list()

alphabetFrequency(dnastring, baseOnly=TRUE, as.prob=TRUE)
#>          A          C          G          T      other 
#> 0.25000000 0.16666667 0.08333333 0.25000000 0.25000000

(Ranged)SummarizedExperiment

Summarized Experiment * Source: https://bioconductor.org/packages/SummarizedExperiment/

(Ranged)SummarizedExperiment

RangedSummarizedExperiment is the de facto standard for “rectangular” data with metadata
Extended by SingleCellExperiment, DESeqDataSet
Emulated by MultiAssayExperiment

Lab Exercises and Links

Lab Exercises
- OSCA Introduction Chapter 3: Getting scRNA-seq datasets. Also note the TENxIO package.
- OSCA Introduction Chapter 4: The SingleCellExperiment class (as time allows)
Links
- A built html version of this lecture is available.
- The source R Markdown is also available from Github.